为了降低难度方便理解,概念先不用管,后面会总结,直接看例子:
下图是B+树的结构,特点是:节点之间含有重复数据,叶子节点还用指针连在一起。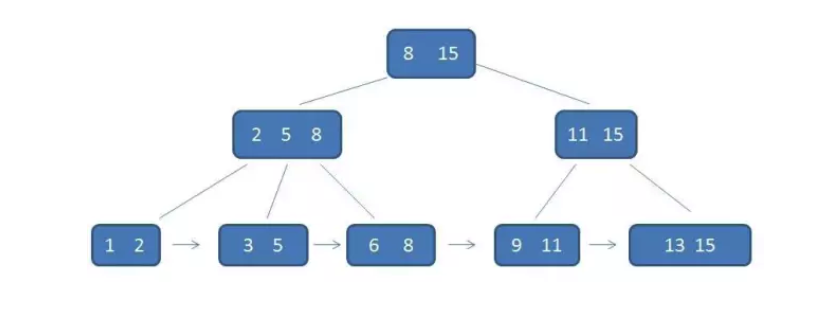
其次,每个父节点的元素都出现在子节点中,是子节点的最大或最小元素。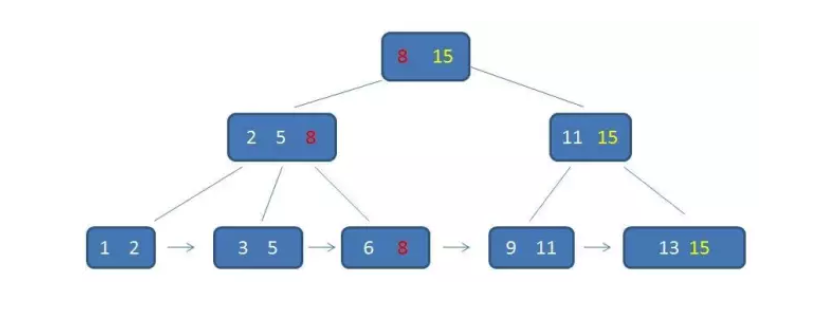
由于父节点的元素都出现在子节点,因此所有叶子节点包含了全量元素信息,并且每个叶子节点都带有指向下一节点的指针,形成了一个有序链表。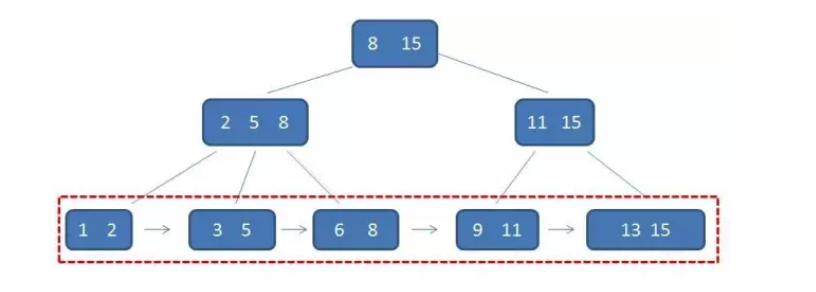
卫星数据:指的是索引元素所指向的数据记录,比如数据库中的某一行。
在B-树中,无论中间节点还是叶子节点都带有卫星数据:
而在B+树中,只有叶子节点带有卫星数据,其余中间节点仅仅是索引,没有任何数据关联: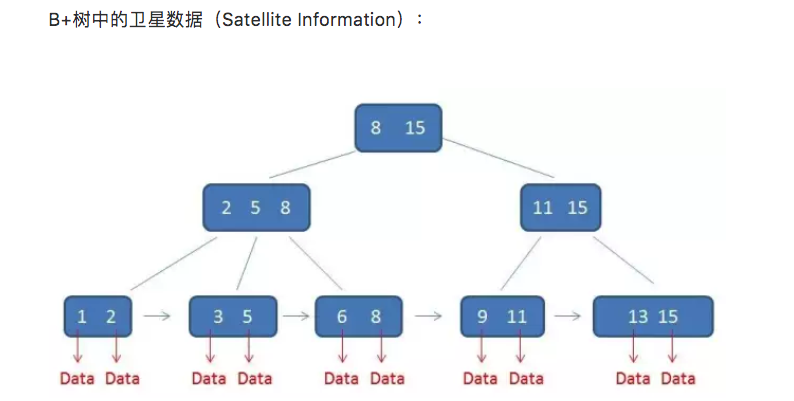
补充一个知识点:在数据库的聚集索引(Clustered Index)中,叶子节点直接包含卫星数据。在非聚集索引(NonClustered Index)中,叶子节点带有指向卫星数据的指针。
B+树设计成这样的好处主要体现在查询性能上,分两种情况讨论:
1.单行查询
单行查询的时候,B+树会自顶向下逐层查找节点,最终找到匹配的叶子节点。比如我们要查找的是元素3: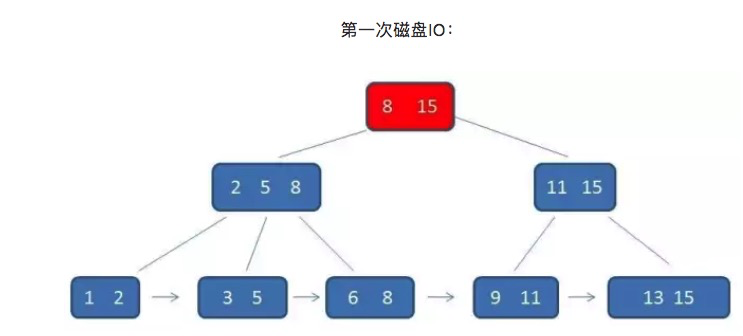
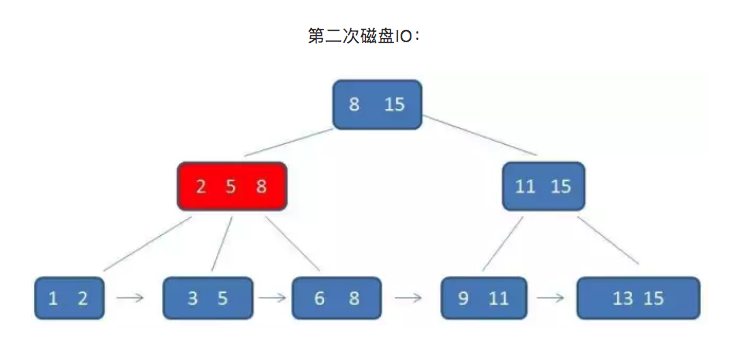
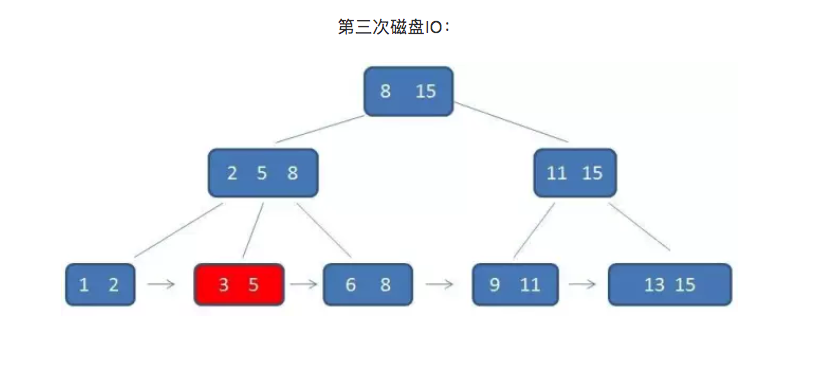
流程看起来和B-树差不多,但是有两点不同。
首先B+树的中间节点没有卫星数据,所以同样大小的磁盘页可以容纳更多的节点元素。这意味着,数据量相同的情况下,B+树的结构比B-树更加“矮胖”(可以理解为树的高度降低了,想象下矮胖的雪人和圣诞树),因此查询时IO次数也更少。
其次,B+树的查询必须最终查找到叶子节点,而B-树只要找到匹配元素即可,无论元素处于中间节点还是叶子节点。因此,可以说B-树的查找性能并不稳定(最好情况是查根节点,最坏情况是查到叶子节点)。而B+树的每一次查找都是稳定的。
2.范围查询
B-树只能依靠繁琐的中序遍历。比如我们要查询范围为3到11元素: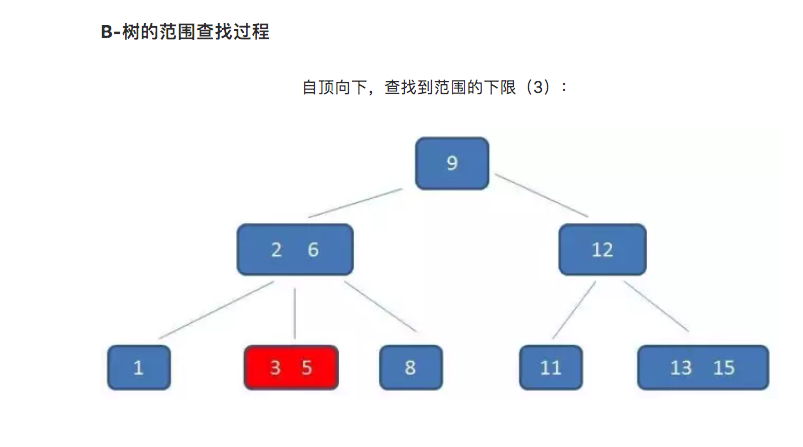
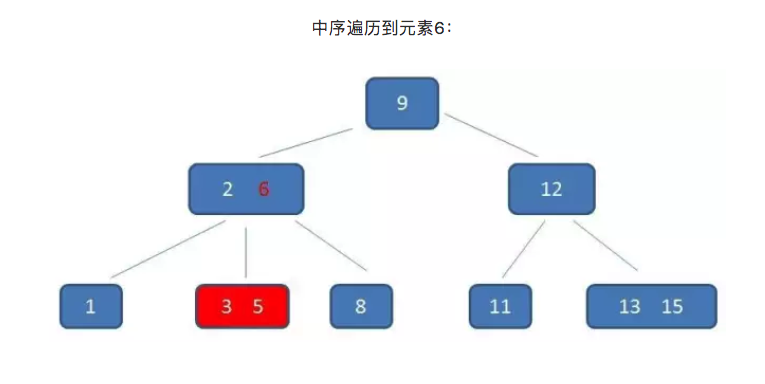
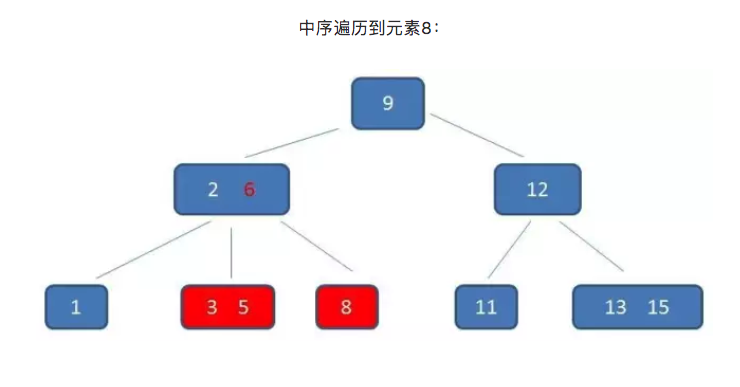
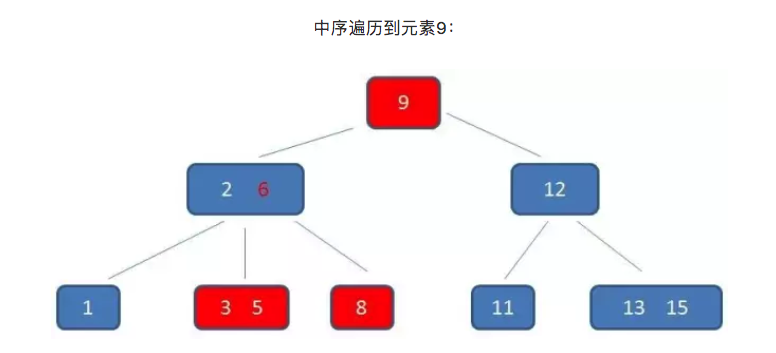
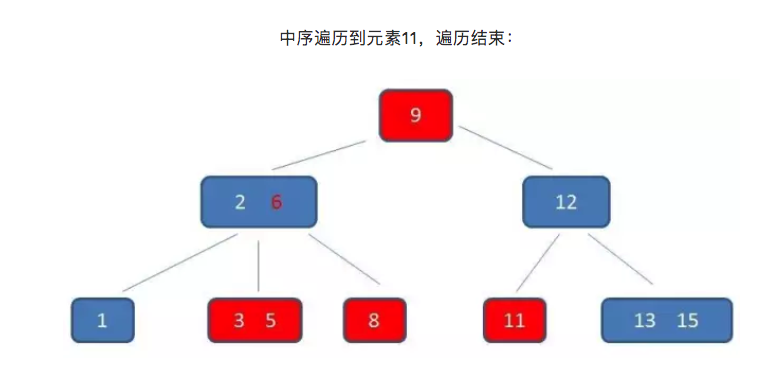
而B+树的范围查询,则要简单得多,只需要在链表上做遍历即可: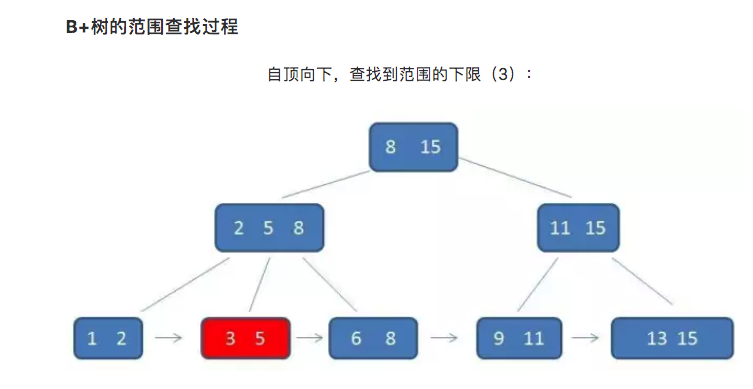

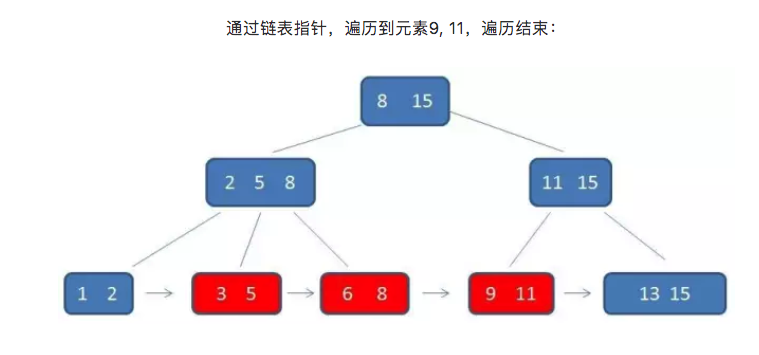
是不是简单很多?
至于B+树的插入和删除,过程与B-树大同小异,不再详解。
最后还是要说下B+树特征的专业偏抽象描述:
1.有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
2.所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
3.所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
最后的最后,总结下B+树的优势:
1.单一节点存储更多的元素,使得查询的IO次数更少。
2.所有查询都要查找到叶子节点,查询性能稳定。
3.所有叶子节点形成有序链表,便于范围查询。
你的Q&A:
1.既然B+树这么好,还要B-树何用???(微笑脸)
B-树的好处是,虽然查询性能不稳定,但平均的查询速度快一些(不用每次都查找到叶子节点为止)
2.如何理解B+树“查询性能稳定”?
B+树的查询每次都查到叶子节点,所以IO次数稳定。试想一个数据库的查询,有时候执行10毫秒,有时候执行100毫秒,肯定是不太合适的。还不如每次都执行30毫秒。
3.看起来和跳跃表有点像?
确实有点像呢,不过跳跃表的层数比B+树更多。可以比较下我另一篇跳跃表的文章。
4.这算不算是以空间换时间呢?
的确是以空间换时间。父节点元素在子节点重复出现,增加了少量空间,换来的是范围查询的便利。
5.HashMap为什么不把红黑树改成b树?
因为二叉查找树的查找效率是最高的,如果内存能装下完整的树,最好使用二叉查找树,b树是退而求其次的方式。
部分内容参考自公众号:程序员小灰


